Today I read for the second time about a simple random-number generator developed by Intel, based on a simple digital circuit:
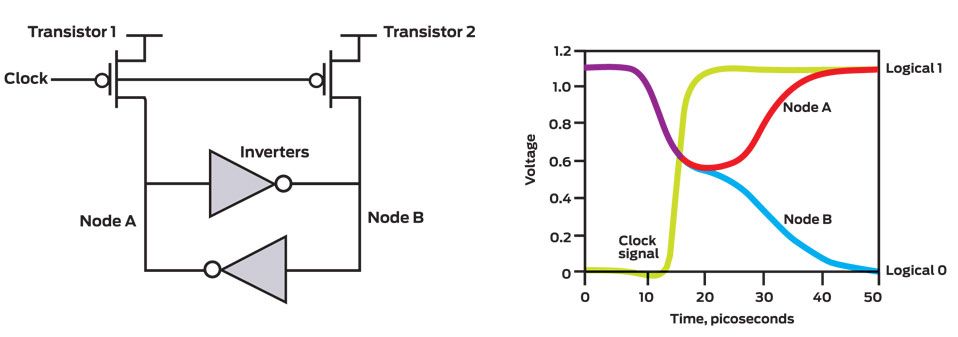
The idea is that initially both inverters leave the circuit in the same state. When the clock pulses both inverters fall into an undeterminate state, and then random noise makes one of the node to switch to a 1, and the other, to 0. One thing that caught my attention on the article was this part:
This digitized approach to random-bit generation would work fine if all inverter circuits were absolutely identical. But the messiness of the physical world never really allows that. In reality, no two inverters are exactly the same. Having subtle differences in the speed or strength of their responses might seem like a mild offense, but in this application, such differences could easily compromise the randomness we were trying to extract from the circuit.
To keep the inverters in balance, we built a feedback loop into the new hardware. The circuitry in that loop performs some targeted fiddling until the two possible output values, 0 and 1, each occur roughly half the time. This helps our design satisfy one of the rules for statistical randomness: In a long stream of numbers, there should be roughly the same number of all possible digits. By adjusting the internal workings of each inverter on the fly, we can defend against the predictability that cryptologists so dread.
I wonder if it wouldn't be feasible to use von Neumann's method of tossing a biased coin?